缩点

CJY2025/5/5大约 9 分钟

缩点

模板题：P3387【模板】缩点

算法介绍

概念

缩点（Contraction of Strongly Connected Components）是图论中对有向图进行简化的重要操作，其核心是将图中的强连通分量（SCC）合并为单个节点。

强连通分量定义：在有向图中，若任意两个节点 $u$ 和 $v$ 之间存在双向路径，则这些节点构成强连通分量。该分量是满足此条件的极大节点集合。

Tarjan 算法由计算机科学家 Robert Tarjan 于 1972 年提出，是一种基于深度优先搜索（DFS）的图论算法，主要用于求解有向图的强连通分量、无向图的割点、无向图的桥。

拓扑排序是对有向无环图（DAG）顶点的一种线性序列化方法，使得对于任何的顶点 $u$ 到 $v$ 的有向边 (u,v) , 都可以有 $u$ 在 $v$ 的前面。

流程

Tarjan（参考 OI-wiki）

Tarjan 算法基于对图进行深度优先搜索。我们视每个连通分量为搜索树中的一棵子树，在搜索过程中，维护一个栈，每次把搜索树中尚未处理的节点加入栈中。

在 Tarjan 算法中为每个结点 $u$ 维护了以下几个变量：

$dfn_u$ 深度优先搜索遍历时结点 $u$ 被搜索的次序。
$low_u$ $l o w_{u}$ 在 $u$ $u$ 的子树中能够回溯到的最早的已经在栈中的结点。
设以 $u$ $u$ 为根的子树为 $Subtree_u$ $S u b t re e_{u}$ 。定义为以下结点的最小值：
- $Subtree_u$ 中的结点
- 从通过一条不在搜索树上的边能到达 $Subtree_u$ 的结点。

按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索，维护每个结点的 $dfn$ 与 $low$ 变量，且让搜索到的结点入栈。每当找到一个强连通元素，就按照该元素包含结点数目让栈中元素出栈。在搜索过程中，对于结点 $u$ 和与其相邻的结点 $v$ （ $v$ 不是 $u$ 的父节点）考虑三种情况：

$v$ 未被访问：继续对 $v$ 进行深度搜索。在回溯过程中，用 $low_v$ 更新 $low_u$ 。因为存在从 $u$ 到 $v$ 的直接路径，所以 $v$ 能够回溯到的已经在栈中的结点， $u$ 也一定能够回溯到。
$v$ 被访问过，已经在栈中：根据 $low$ 值的定义，用 $dfn_v$ 更新 $low_u$ 。
$v$ 被访问过，已不在栈中：说明 $v$ 已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

这么说不是很直观，用一个例子演示：

12 21
1 2 3 4 5 6 7 8 9 10 11 12
1 2
2 3
3 4
4 1
5 6
6 5
7 8
8 9
9 7
4 5
6 7
9 10
10 11
11 12
12 11
12 9
3 7
1 5
5 7
7 10
10 12

下面这张动图演示了 Tarjan 算法的流程，其中黑色数字是结点编号（为了方便， $dfn$ 和点权也是同样的数字），红色数字是 $low$ ，被彩色笔圈起来表示出栈了，不同颜色代表不同强连通分量。这个例子中，一共有三个强连通分量。

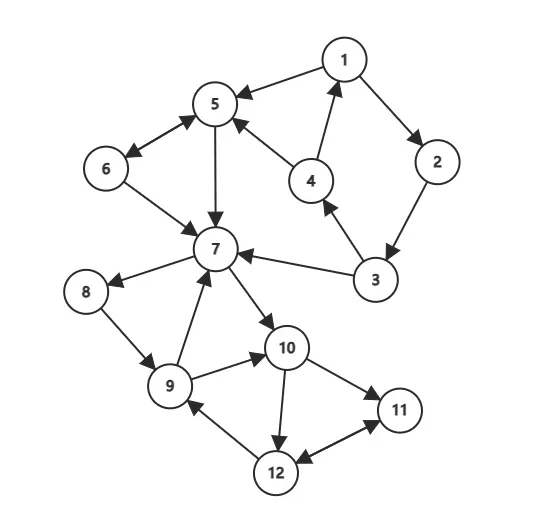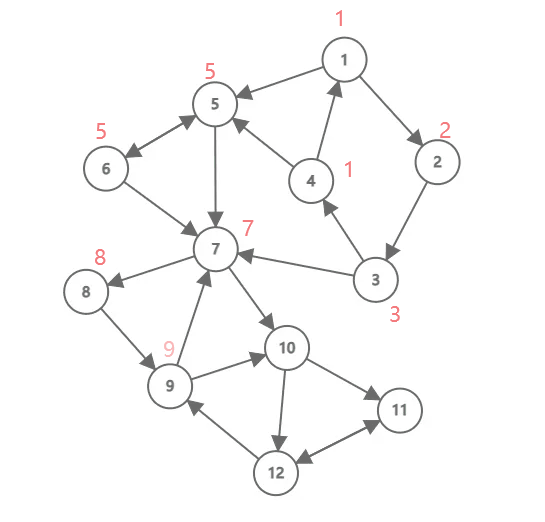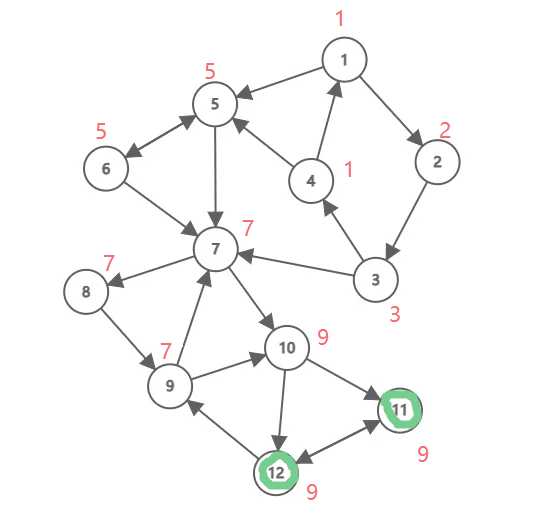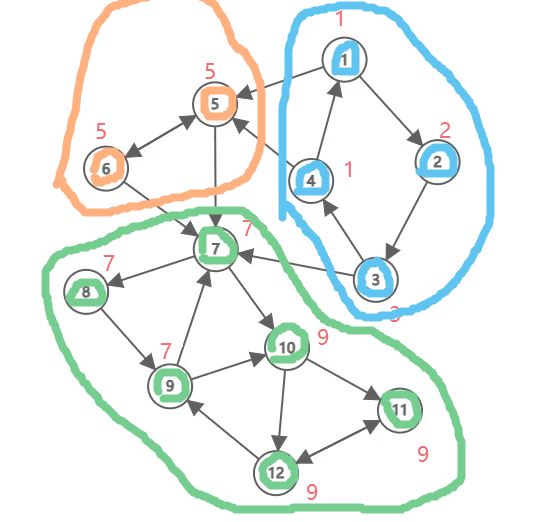
对于一个连通分量图，我们很容易想到，在该连通图中有且仅有一个 $u$ 使得 $dfn_u=low_u$ 。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 $dfn$ 和 $low$ 值最小，不会被该连通分量中的其他结点所影响。

因此，在回溯的过程中，判定 $dfn_u=low_u$ 是否成立，如果成立，则栈中 $u$ 及其上方的结点构成一个强连通分量。

缩点

看标题就知道，这是本题的关键。为什么要缩点呢？因为这张图不是 DAG（有向无环图），无法通过 DP 的方式求出答案。仔细思考一下，既然一个强连通分量里所有的点都可以互相到达，我们就可以不用管它的内部结构，直接把它当作成一个点，不就行了吗。这就是缩点。别忘了融合后的点权值是所在强连通分量里所有点的权值之和。缩点之后，这张图变成了一个 DAG，就可以求了。

至于怎么缩点，可以建一个新图，把融合后的点和连接两个不同强连通分量的边加入新图就可以了。

缩好点后的图长这样，是一个 DAG：

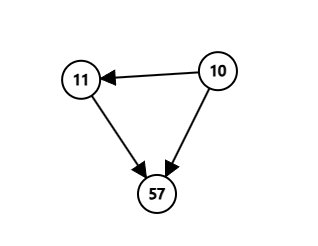
用肉眼就能很容易看出来，这幅图答案为 $78$ 。

拓扑排序

有人可能不知道为什么拓扑排序可以求 DAG 的最大权值路径的权值。它其实是和 DP 有关的，用类似 Bellman-Ford 的松弛，写出状态转移方程：

dp_v=\max(dp_v,dp_u+a_v)

而 DP 执行的顺序，就是拓扑排序的顺序。

答案就是 $\max_{i=1}^n dp_i$ 。

拓扑排序的流程想必大家都会，不会可以看 OI-wiki，我就不过多介绍了。

正确性证明

强连通分量（SCC）缩点的正确性

性质：一个强连通分量内的所有节点可以互相到达。因此，若路径经过该分量中的任意节点，总能调整路径使其访问分量内所有节点（从而权值总和固定为该分量的权值之和）。
权值合并：将每个 SCC 的权值设为内部所有节点权值之和。无论路径如何经过该分量，权值贡献最大化为该总和，重复访问不会增加权值。
路径映射：原图中的路径对应缩点后 DAG 中的路径。例如，原路径 A→B→C（B、C属于同一 SCC）会被映射为 A→SCC_B，而 SCC_B 的权值包含 B、C 的权值总和。

DAG 构造的正确性

无环性：SCC 之间不存在循环依赖，否则这些 SCC 会被合并为一个更大的 SCC 。因此，缩点后的图是 DAG 。
拓扑序的可行性：DAG 的拓扑排序能保证处理节点时，所有前驱节点的状态已计算完成，为动态规划提供基础。

合并 SCC 权值：遍历每个节点，累加其所属 SCC 的权值，复杂度 $O(n)$ 。
建立 DAG 边：遍历原图所有边，若两端点属于不同 SCC，则在对应 SCC 间添加边，复杂度 $O(m)$ 。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10, M = 1e5 + 10; //点数和边数
int n, m, a[N], u[M], v[M];
vector<int> g[N], g2[N]; //vector存图
int dfn[N], low[N], cnt = 0, stk[N], top=0, instk[N], belong[N];
//cnt记录访问次序，stk是栈，top栈顶，instk是否在栈里，belong属于哪个强连通分量
int in[N], dp[N], ans=0; //in入度，dp动态规划，ans答案
void tarjan(int u) { //tarjan算法
	dfn[u] = low[u] = ++cnt, stk[++top] = u, instk[u] = 1;
	for(auto i : g[u]) { //遍历下一个点
		if(!dfn[i]) { //没有访问过
			tarjan(i); //去递归它
			low[u] = min(low[u], low[i]); //更新low值
		}
		else if(instk[i]) //访问过且在栈中
			low[u] = min(low[u], dfn[i]); //更新low值
	}
	if(dfn[u] == low[u]) { //找到一个SCC
		do {
			instk[stk[top]] = 0; //出栈
			belong[stk[top]] = u; //这个结点属于u代表的SCC
			if(stk[top] != u) a[u] += a[stk[top]]; //缩点累加权值
		}while(stk[top--] != u); //循环直到栈顶是自己
	}
}
void topo() { //拓扑排序
	queue<int> q;
	for(int i = 1; i <= n; i++) {
		if(i == belong[i] && !in[i]) { //找到一个入度为零的点且代表SCC
			q.push(i); //入队
			dp[i] = a[i]; //初始化dp
		}
	}
	while(!q.empty()) {
		int s = q.front(); q.pop(); //类似广搜
		for(auto i : g2[s]) { //枚举下一个点
			dp[i] = max(dp[i], dp[s] + a[i]); //状态转移
			if(--in[i] == 0) q.push(i); //入度为零就入队
		}
	}
}
int main() {
	cin >> n >> m;
	for(int i = 1; i <= n; i++)
		cin >> a[i];
	for(int i = 1; i <= m; i++) {
		cin >> u[i] >> v[i];
		g[u[i]].push_back(v[i]);
	}
	for(int i = 1; i <= n; i++)
		if(!dfn[i]) tarjan(i); //tarjan
	for(int i = 1; i <= m; i++) { //缩点
		int x = belong[u[i]], y = belong[v[i]];
		if(x != y) { //边的两个顶点不同才被放进新图中
			g2[x].push_back(y);
			in[y]++; //统计入度
		}
	}
	topo(); //拓扑排序
	for(int i = 1; i <= n; i++)
		ans = max(ans, dp[i]); //统计dp答案
	cout << ans; //输出答案
	return 0; //好习惯
}

高清无注释

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10,M=1e5+10;
int n,m,a[N],u[M],v[M];
vector<int>g[N],g2[N];
int dfn[N],low[N],cnt=0,stk[N],top=0,instk[N],belong[N];
int in[N],dp[N],ans=0;
void tarjan(int u){
	dfn[u]=low[u]=++cnt,stk[++top]=u,instk[u]=1;
	for(auto i:g[u]){
		if(!dfn[i]){
			tarjan(i);
			low[u]=min(low[u],low[i]);
		}
		else if(instk[i])
			low[u]=min(low[u],dfn[i]);
	}
	if(dfn[u]==low[u]){
		do{
			instk[stk[top]]=0;
			belong[stk[top]]=u;
			if(stk[top]!=u)a[u]+=a[stk[top]];
		}while(stk[top--]!=u);
	}
}
void topo(){
	queue<int>q;
	for(int i=1;i<=n;i++){
		if(i==belong[i]&&!in[i]){
			q.push(i);
			dp[i]=a[i];
		}
	}
	while(!q.empty()){
		int s=q.front();q.pop();
		for(auto i:g2[s]){
			dp[i]=max(dp[i],dp[s]+a[i]);
			if(--in[i]==0)q.push(i);
		}
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	for(int i=1;i<=m;i++){
		cin>>u[i]>>v[i];
		g[u[i]].push_back(v[i]);
	}
	for(int i=1;i<=n;i++)
		if(!dfn[i])tarjan(i);
	for(int i=1;i<=m;i++){
		int x=belong[u[i]],y=belong[v[i]];
		if(x!=y){
			g2[x].push_back(y);
			in[y]++;
		}
	}
	topo();
	for(int i=1;i<=n;i++)
		ans=max(ans,dp[i]);
	cout<<ans;
	return 0;
}

后记

此题解法不唯一，你也可以用其他算法实现。

缩点

缩点

模板题：P3387【模板】缩点

算法介绍

概念

流程

Tarjan（参考 OI-wiki）

缩点

拓扑排序

正确性证明

强连通分量（SCC）缩点的正确性

DAG 构造的正确性

tarjan

时间复杂度证明

Tarjan

缩点构建 DAG

拓扑排序和 DP

总复杂度

代码